Alpha-bêta ou l'algo qui a battu le champion du monde aux échecs

Introduction

Le 11 Mai 1997, pour la première fois dans l'histoire, un ordinateur, Deep Blue d'IBM, a battu le champion du monde d'échecs Garry Kasparov dans le cadre d'un tournoi. Cet évènement marqua un tournant décisif dans les débuts de l'intelligence artificielle et des avancées algorithmiques.

Pourtant, il existe environ 10¹²⁰ parties théoriques possibles aux échecs (à un pion près 😅), soit 10⁴⁰ de plus que le nombre d'atomes qui constitue l'Univers observable !

Comment un ordinateur avec des capacités matérielles beaucoup plus limitées que les supercalculateurs d'aujourd'hui a pu déterminer en un temps réalisable les meilleurs coups menant à une victoire quasi certaine ?

L'heure est venue de découvrir (ou redécouvrir ?) les algorithmes MinMax – aussi appelé "minimax" – et l'élagage alpha-bêta, bijoux d'aide à la prise de décision stratégique, même encore aujourd'hui !

L'algorithme de recherche MinMax

Commençons par l'épine dorsale de la théorie des jeux : évaluer tous les coups possibles et les gains théoriques associés. Plaçons-nous justement dans le contexte d'une partie d'échecs entre un joueur humain et un ordinateur.

On souhaite faire gagner l'ordinateur.

Chaque mouvement d'une pièce de l'ordinateur ou du joueur humain conduit à une nouvelle situation de jeu. On peut modéliser ces situations de jeu à travers un arbre :

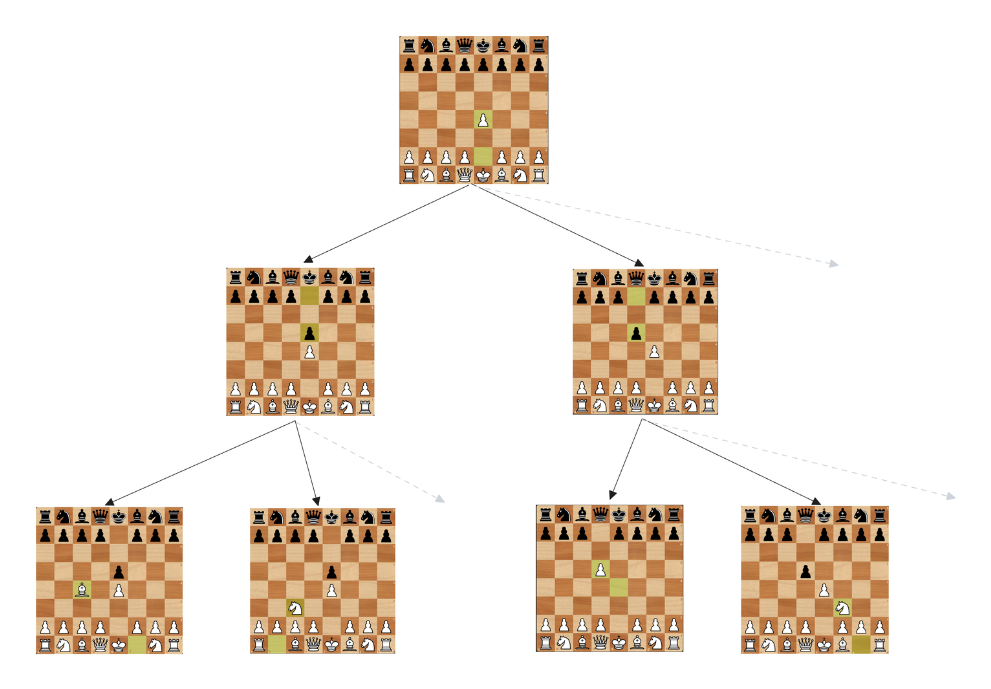
Imaginons maintenant que la partie soit un peu plus avancée, et que ce soit à l'ordinateur de jouer.

Afin de trouver LE meilleur coup possible pour l'ordinateur, on commence par déterminer une profondeur de recherche maximum – ici 3 – puis on construit l'arbre des évolutions du jeu en fonction des coups joués par chaque adversaire :

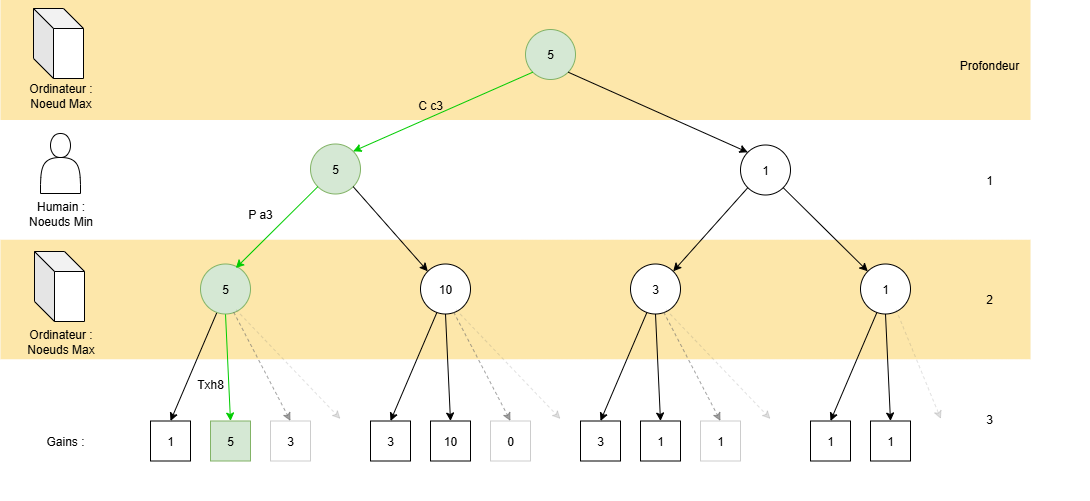
(Si vous n'êtes pas familier de la notation algébrique des coups aux échecs "Cc3, Pa3, ...", vous pouvez toujours aller jeter un œil ici, mais ce n'est pas indispensable pour comprendre l'algorithme dans cet article.)

Chaque nœud est un choix de coup parmi toutes les branches descendantes directes.

On appelle nœuds Max les décisions prises par l'ordinateur à son tour de jeu. En effet, étant donné que l'on souhaite le faire gagner, nous allons lui faire jouer les meilleurs coups (donc gain Maximal).

A contrario, on dit que c'est un nœud Min lorsque c'est au joueur humain de jouer, car on considère qu'il va jouer le coup le plus défavorable dans l'intérêt de l'ordinateur, et donc Minimiser les gains de son adversaire.

Arrivés à la profondeur maximale, on calcule le gain qu'offre chaque situation de jeu atteinte.

Le gain peut-être estimé de différentes façons : gain matériel, positionnel, victoire par mat, égalité par pat, etc. Pour simplifier l'explication, nous modéliserons le gain par une simple valeur qui peut très bien représenter la valeur d'une prise. Par exemple, prendre une Tour (valeur 5) donnera un gain matériel supérieur à la prise d'un Pion (valeur 1).

Notez également que seuls quelques coups seront traités dans notre exemple. Tous les autres coups possibles seront représentés par les flèches en pointillé et ne seront pas évalués dans l'algorithme (sinon imaginez la tête du schéma 😜).

En remontant tous les gains du bas vers le haut de l'arbre avec cette logique, on peut alors conclure que le meilleur coup à jouer pour l'ordinateur dans la situation de départ sera Cc3 👍 (et donc le cavalier en c3).

Seulement voilà, comme on peut le constater, l'arbre peut rapidement devenir gigantesque, même en limitant la profondeur de recherche. Et les calculs de gains peuvent nécessiter des algorithmes lourds si on ne se limite pas à un gain matériel. Il faudrait trouver un moyen de réduire cette complexité d'exploration.

Mais d'ailleurs, en y réfléchissant bien, est-il réellement nécessaire d'explorer absolument tous les nœuds ? 🤔

L'optimisation par élagage alpha-bêta

L'idée de cette optimisation est simple : si nous sommes capables d'affirmer avec certitude qu'une branche ne changera pas la valeur d'un nœud Min parent ou d'un nœud Max parent, il est alors inutile d'aller explorer cette branche enfant et de calculer ses gains. On peut alors l'élaguer.

Eh oui ! Quel intérêt d'envisager ce que donnerait la partie en prenant un Pion, si nous venons de trouver un autre coup qui permet de prendre une Dame ? (toujours dans une logique purement matérielle)

Pour appliquer cette optimisation, on définit deux variables α et β dont les valeurs se transmettent de parent à enfant dans l'arbre :

- α contient la valeur maximale rencontrée par les nœuds Max, et ne sera mis à jour que sur des nœuds Max ;

- β contient la valeur minimale rencontrée par les nœuds Min, et ne sera mis à jour que sur des nœuds Min

On fixe la règle suivante : si dans un nœud α > β, alors on élague les branches enfants non explorées sous ce nœud. Pas la peine d'aller plus loin ! 🫥

Voyons concrètement ce que cela donne avec notre partie d'échec :

1. En parcourant la branche de gauche (Cc3) on transmet α et β à chaque nœud avec leurs valeurs initiales respectives <span class="css-span">-infini</span> et <span class="css-span">+infini</span>.

2. On commence à évaluer les gains tout en bas à gauche. Puisque c'est un nœud Max, on met à jour α qui vaut maintenant 5, car <span class="css-span">5 > -infini</span>.

3. On remonte le gain au nœud parent (le nœud Min 5). Puisque c'est un nœud Min, on met à jour β qui vaut alors 5, car <span class="css-span">5 < +infini</span>.

4. On redescend les valeurs α et β dans le deuxième nœud enfant, et en déterminant seulement les gains 3 et 10, on se rend compte que α > β (car <span class="css-span">10 > 3 > -infini</span> pour α). Alors on peut se permettre d'élaguer les autres branches à droite du nœud 10 sans même les regarder !

De la même manière, on remonte le gain 5 au premier nœud tout en haut en mettant à jour α, car c'est un nœud Max :

Et on réapplique la même logique sur les branches de droite !

On remarque très vite que sur le nœud Min 1 de droite, α > β. Bim ! On peut appliquer un deuxième élagage de toute la partie droite ! 😎

Bilan ? Avec ces deux élagages, nous venons d'économiser 3 calculs de gains sur 11, si on ne compte que les coups visibles sur le schéma. Soit environ 30 % de complexité en moins sur l'algorithme MinMax initial !

Le mot de la fin

Nous venons de comprendre comment un problème à explosion combinatoire peut être simplifié jusqu'à une échelle devenue résoluble. Un des secrets de la victoire de l'ordinateur Deep Blue, donc.

L'élagage alpha-bêta est d'ailleurs d'autant plus efficace qu'il y a de possibilités à chaque nœud. Ce qui est une aubaine pour des modèles plus riches et plus ancrés dans la réalité.

Depuis la victoire de Deep Blue, d'autres techniques d'élagage ont vu le jour dans d'autres domaines, comme la PVS (Principal Variation Search) ou les élagages probabilistes, comme dans certaines IA d'aujourd'hui où l'approche peut être plus heuristique.

Outre les échecs, les algorithmes MinMax sont utilisés aujourd'hui dans bien d'autres cas d'application comme la prise de décision en robotique, des scénarios politiques, la gestion des risques financiers, etc.

Tant que la meilleure décision est gardée à la fin… 😄

‍